Domes and frame structures¶
Hesperia dome¶
The Hesperia dome is a enormous construction made of glass on top of a hotel in Barcelona. With pyFormex, a parametric 3D model of this dome was created which allowed to evaluate geometric variations changing one or more parameters (e.g. the span or height of a dome, the amount of secondary triangles, etc.) as shown in the figure below. As illustrated, geometries can be displayed in several ways (e.g. wireframe, flat, smooth, transparent). Automated generation of finite element input files can be incorporated in pyFormex.

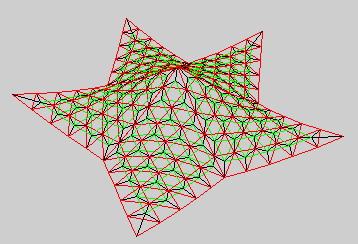
Hyparcap¶
A space frame in the form of a five-pointed star of hypars.
Scallop dome¶
Example showing the parametric capabilities of pyFormex. Both domes are createdby the same small script, by only changing two parameters.


SpaceTrussRoof¶
A space truss used for the roof of an industrial building.

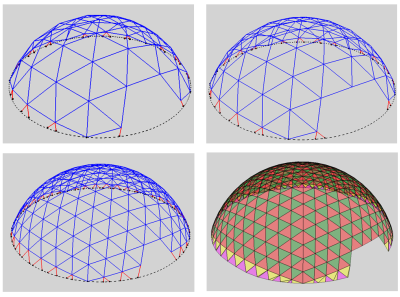
Geodesic Dome¶
This example illustrates the use of surface elements. It shows four steps in the creation of a geodesic dome.

First we create two triangles. We give them different colors so that they are easy to distinguish:
v=0.5*sqrt(3.)
a = Formex([[[0,0],[1,0],[0.5,v]]],1)
aa = Formex([[[1,0],[1.5,v],[0.5,v]]],2)

Next we copy the triangles a number of times in two directions, generating the triangular pattern at the left:
m=5; n=5
d = a.replic2(m,min(m,n),1.,v,bias=0.5,taper=-1)
dd = aa.replic2(m-1,min(m-1,n),1.,v,bias=0.5,taper=-1)

Then we copy-rotate the pattern into a hexagon:
e = (d+dd).rosette(6,60,point=[m*0.5,m*v,0])

Lastly the pattern is mapped on a sphere, resulting in a geodesic dome from which we give a perspective view:
f = e.mapd(2,lambda d:0.8*sqrt((m+1)**2-d**2),e.center(),[0,1])

